(期权价值评估2)
第七章 期权价值评估
四、金融期权价值的评估方法
(一)期权估值原理
1.复制原理
复制原理的步骤如下:

【注】利率要折合为同等期间的利率,如题目告诉年利率4%,而期权6个月后到期,则这里的利率=4%/2=2%.
|
【例题13·计算题】假设A公司的股票现在市价为50元,有一股以该股票为标的资产的看涨期权,执行价格为52.08元,到期时间是6个月。6个月以后股价有2种可能:上升33.33%,或者下降25%,借款利率(无风险利率)为每年4%。通过建立一个投资组合,包括购进适当的股票以及借入必要的款项,求6个月后到期的看涨期权的价值? 【解析】 (1)确定6个月后股票可能的价格。Su=S0×u=50×(1+33.33%)=66.66(元);Sd= S0×d=50×(1-25%)=37.5(元)。 (2)确定看涨期权的到期日价值。Cu=Max(0,Su-X)= Max(0,66.66-52.08)=14.58(元);Cd=Max(0,Sd-X)= Max(0,37.5-52.08)=0(元). (3)建立对冲组合。Su×n-B×(1+r)=Cu ;Sd×n-B×(1+r)=Cd 66.66×n-B×(1+2%)=14.58;37.5×n-B×(1+2%)=0;解得B=18.38(元)、n=0.5(股) (4)看涨期权价格即为购建组合成本。看涨期权价格=组合成本=n×S0-B=0.5×50-18.38=6.62(元)。 |
2.套期保值原理
套期保值比率(即求需要购买的股票数量):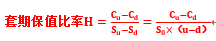
借款数额=(到期日下行股价×套期保值比率-股价下行时期权到期日价值)÷(1+r)
运用套期保值原理求看涨期权价格,和复制原理步骤一样,唯一区别就是,求解建立的对冲组合方法不一样。
【注】Cd通常都为零,故,无需计算。
3.风险中性原理
风险中性的步骤如下:


|
【解析】 (1)求上行概率。 期望报酬率=2%=上行概率×33.33%+下行概率×(-25%)=上行概率×33.33%+(1-上行概率)×(-25%) 上行概率=0.4629,下行概率=1-0.4629=0.5371 (2)求期权到期后的期望价值。C=0.4629×14.59+0.5371×0=6.75(元) (3)求期权的现值。期权现值=6.75÷(1+2%)=6.62(元) |
(二)二叉树期权定价模型
二叉数期权定价模型的假设基础:①市场投资没有交易成本;②投资者都是价格的接受者;③允许完全使用卖空所得款项;④允许以无风险利率借入或贷出款项;⑤未来股票的价格将是两种可能值中的一个。
1.单期二叉树期权定价模型

|
要求:利用单期二叉树定价模型确定期权的价值。 【答案】 Cu=Max(0,Su-X)= Max(0,20×(1+40%)-21)=7(元)
|
(三)看涨期权-看跌期权平价定理
对于欧式期权,假定看涨期权和看跌期权有相同的执行价格和到期日,则下述等式成立:
看涨期权价格C-看跌期权价格P=标的资产的价格S-执行价格的现值PV(X)
利用该等式中的4个数据中的3个,就可以求出另外1个。
【注意】美式期权在到期前的任意时间都可以执行,除享有欧式期权的全部权利之外,还有提前执行的优势。因此,美式期权的价值应当至少等于相应欧式期权的价值,在某种情况下比欧式期权的价值更大。
|
【例题15·计算题】两种期权的执行价格均为30元,6个月到期,6个月的无风险报酬率为4%,股票的现行价格为35元,看涨期权的价格为9.20元,求看跌期权的价格为多少? 【答案】根据C-P=S-PV(X),得到: P=C-S+PV(X)=9.20-35+30÷(1+4%)=9.20-35+28.8=3(元) |
|
A.6.89 B.13.11 C.14 D.6 【答案】C 【解析】20+看跌期权价格=10+24.96/(1+4%),所以看跌期权价格=14元。 |
|
要求: (1)利用风险中性原理,计算看涨期权的股价上行时到期日价值、上行概率及期权价值,利用看涨期权-看跌期权平价定理,计算看跌期权的期权价值。 (2)假设目前市场上每份看涨期权价格2.5元,每份看跌期权价格6.5元,投资者同时卖出1份看涨期权和1份看跌期权,计算确保该组合不亏损的股票价格区间,如果6个月后,标的股票价格实际上涨20%,计算该组合的净损益。(注:计算股票价格区间和组合净损益时,均不考虑期权价格的货币时间价值)(2015年试卷Ⅱ) 【答案】(1)看涨期权的股价上行时到期日价值=40×(1+25%)-45=5(元) 2%=上行概率×25%+(1-上行概率)×(-20%) 即:2%=上行概率×25%-20%+上行概率×20% 则:上行概率=0.4889 由于股价下行时到期日价值=0 所以,看涨期权价值=(5×0.4889+0.5111×0)/(1+2%)=2.4(元) 看跌期权价值=45/(1+2%)+2.4-40=6.52(元) (2) 卖出看涨期权的净损益=-Max(股票市价-执行价格,0)+期权价格=-Max(股票市价-45,0)+2.5 卖出看跌期权的净损益=-Max(执行价格-股票市价,0)+期权价格=-Max(45-股票市价,0)+6.5 组合净损益=-Max(股票市价-45,0)-Max(45-股票市价,0)+9 因要求组合不归亏损,故 当股价>执行价格时:组合净损益=0=-(股票市价-45)+9,股票市价=54(元) 当股价<执行价格时:组合净损益=0=-(45-股票市价)+9,股票市价=36(元) 所以,确保该组合不亏损的股票价格区间为36元~54元。 如果6个月后的标的股票价格实际上涨20%,即股票价格为40×(1+20%)=48(元),则:组合净损益=-(48-45)+9=6(元)。 |
阅读列表
-
(财务报表分析和预测)
2018/9/14 · 234人已阅
-
(业绩评价+管理会计报告)
2018/9/11 · 191人已阅
-
(责任会计)
2018/9/07 · 211人已阅
-
(短期经营决策+全面预算)
2018/9/05 · 206人已阅
-
(本量利分析)
2018/8/31 · 199人已阅
-
(作业成本法)
2018/8/28 · 310人已阅
-
(标准成本法)
2018/8/23 · 277人已阅




