第三章 价值评估基础

一、利率期限结构（18年有改动）

二、货币时间价值

有效年利率=（1+报价利率/m）^m-1（有效年利率大于等于报价利率）

计息期利率==报价利率/每年复利次数

二、风险与收益

1.变异系数

变异系数=标准差/均值

2.协方差

协方差σ_jk=r_jkσ_jσ_k

相关系数=σ_jk/σ_jσ_k

相关系数∈[-1,1]，r=1，正相关；r=-1,负相关；r=0，无关。

3.投资组合的风险衡量

组合的收益是单项证券收益的加权平均数，但风险不是，风险还取决于组合内各个证券之间的关系。

投资组合可以降低风险，但不能完全消除风险，证券种类越多，非系统风险越小。

影响组合的标准差不仅取决于单个证券的标准差，还取决于证券之间的协方差。充分投资组合的风险，只受证券之间协方差的影响，而与各证券本身的方差无关。

4.投资机会集曲线（描述了不同投资比例组合的风险和报酬之间的权衡关系）

r<1，机会集弯曲，有分散风险的效应；

r足够小，风险分散效应越强，会产生最小方差组合，会出现无效集

注意：并不是一定存在拐点和无效集。如果相关系数没有小到一定程度，则没有拐点和无效集出现，则最小方差组合是将资产全部投资于报酬率和风险较低的证券种类。

5.资本市场线

假设存在无风险资产，投资者也能够买入或者卖出时无风险资产和风险资产的机会集曲线

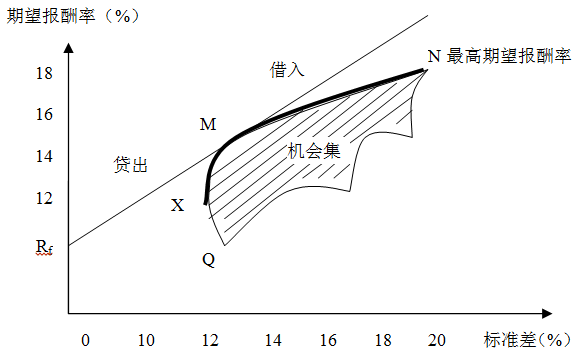
从无风险资产的报酬率开始，做有效边界的切线，切点为M，该直线被称为资本市场线。

（1）总期望报酬率=Q×（风险组合的期望报酬率）+（1-Q）×（无风险报酬率）

总标准差=Q×风险组合的标准差

（Q代表投资者自有资本总额中投资于风险组合的比例，“1-Q”代表投资于无风险资产的比例。如果贷出资金，Q将小于1；如果是借入资金，Q会大于1）

（2）切点M为市场平衡点，代表唯一最有效的风险资产组合，此时全部自有资金投资于风险资产组合

（3）解释了持有不同比例无风险资产与市场组合情况下风险和期望报酬率的关系。在M点的左侧，你将同时持有无风险资产和风险资产组合。在M点的右侧，你将仅持有风险资产组合M，并且会借入资金以进一步投资于风险资产组合M。

（4）个人的效用偏好与最佳风险资产组合相独立。投资者个人对风险的态度仅仅影响借入或贷出的资金量，而不影响最佳风险资产组合。

6.系统风险和非系统风险

系统风险: 是指那些影响所有公司、所有资产、整个市场的风险。例如：地震，战争、经济危机等，不能通过投资组合消除

非系统风险：企业特有风险，特定企业或特点行业所特有，可通过增加资产组合中资产数量来消除

（1）单项资产的β系数：某个资产的收益率与市场组合之间的相关性，衡量的是系统风险。

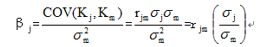
由于资产组合不能抵消系统风险，所以资产组合的β数是单项资产β的加权平均数。

（2）市场组合相对于它自己的贝塔系数是1。

β=1，表示该资产的系统风险程度与市场组合的风险一致；

β＞1，说明该资产的系统风险程度大于整个市场组合的风险；

β＜1，说明该资产的系统风险程度小于整个市场投资组合的风险；

β=0，说明该资产的系统风险程度等于0。

（3）大小取决于：该股票与整个股票市场的相关性、它自身的标准差、整个市场的标准差

7.资本资产定价模型（CAMP模型）

必要收益率=无风险收益率+风险附加率：R_i=R_f+β×（R_m-R_f）（所代表的直线就是证券市场线）

市场风险溢价率（R_m-R_f）（市场风险补偿率）反映市场整体对风险的偏好，如果风险厌恶程度高，则证券市场线的斜率（R_m-R_f）的值就大。

8. 资本市场线与证券市场线的区别