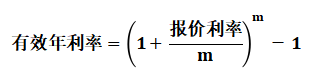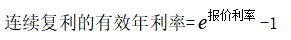【例题1·单选题】下列各项说法中，符合流动性溢价理论的是（    ）。（2018年）

A. 不同期限的债券市场互不相关

B. 长期即期利率是短期预期利率的无偏估计

C. 即期利率水平由各个期限债券市场上的供求关系决定

D. 债券期限越长，利率变动可能性越大，利率风险越高

【答案】D

【解析】选项B符合无偏预期理论；选项A、C符合市场分割理论；选项D符合流动性溢价理论。

含义

关系

报价利率

指一年复利若干次时给出的年利率，也叫名义利率，用r表示。

计息期利率=报价利率/每年复利次数

假设每年计息m次，则

【结论】

当每年计息一次时：有效年利率=报价利率

当每年计息多次时：有效年利率>报价利率

计息期利率

计息期利率是指借款人对每1元本金每期支付的利息。它可以是年利率，也可以是半年利率、季度利率、每月或每日利率等。

有效年利率

在按给定的计息期利率和每年复利次数时，能够产生相同结果的每年复利一次的年利率被称为有效年利率，也称等价年利率。

当复利次数m趋于无穷大时，利息支付的频率比每秒1次还频繁，所得到的利率为连续复利。

e为自然常数。

【例题2·单选题】甲公司平价发行5年期的公司债券，债券票面利率为10%，每半年付息一次，到期一次偿还本金。该债券的有效年利率是（  ）。（2013）

A.10%

B.10.25%

C.10.5%

D.9.5%

【答案】B

【解析】有效年利率=（1+10%/2）²-1=10.25%

【例3·多选题】下列关于货币时间价值系数关系的表述中，正确的有（    ）。（2009年）

A.普通年金现值系数×投资回收系数=1

B.普通年金终值系数×偿债基金系数=1

C.普通年金现值系数×（1+折现率）=预付年金现值系数

D.普通年金终值系数×（1+折现率）=预付年金终值系数

【答案】ABCD

【例4•计算题】某人投资10万元，预计每年可获得25 000元的回报，若项目的寿命期为5年，则投资回报率为多少？

（P/A，7%，5）=4.1002； （P/A，8%，5）=3.9927

【答案】

10=2.5×（P/A，I，5）

（P/A，I，5）=4

（I-7%）/（8%-7%）=（4-4.1002）/（3.9927-4.1002）

I=7.93%